Automatc frequency domain analysis of digital ciruits
This post is about design and analysis of digital circuits using haskell as a language and clash as tool to generate digital circuits.
Main Idea
Frequency analysis can be preformed for digital circuits using only adders, multiplies and register. Intuitive reasoning to get response of single frequency from such circuitry as black box goes as. We insert Signal of complex numbers in circuitry and from resulting complex signal observe phase and amplitude. Registry in this setup is no more than rotation of phase or phase delay that depends on Nyquist frequency of input signal.
Analysis is not done in time, but directly in frequency domain. For one input frequency we get amplitude and phase of output. Approach works best for acyclic circuits, both linear (e.g. fir filter) and nonlinear circuits (e.g. frequency mixer). It can be used for linear cyclic circuits for example iir filter. Anaysis result can be presented as Bode or Nyquist plot. Experimental hacked up implementation is available at github.
Example of use
Clash compiler can be used to both design digital circuitry and analyze them using the great language Haskell. Both in time and frequency domain. Analysis in time domain is part of standard library that ships with distribution.
We can describe fir filter in language haskell for example as:
fir coeffs x = dotp coeffs (windowP x)
where
dotp as bs = sum (zipWith (*) as bs)
This description enables generating digital circuit by compiling in vhdl or verilog language and than burn this in FPGA or in ASIC.
We begin by generating fir coeficients. For example by using python library scipy. There is also haskell library dsp that can do same.
>>> from scipy import signal as s
>>> s.firwin2(101,freq=[0,0.5,0.55,1],gain=[1,1,1e-5,1e-5],nfreqs=1024).tolist()
this generates 101 fir coefficient-s with gain 1 in interval [0,0.55] and gain 1e-5 in interval [0.55,1] where interval represents Nyquist frequency. Nyquist frequency is frequency scaled from 0 to 1/2 of sampling frequency.
firCoef = -6.478374934754401e-05 :> 6.739792048055188e-05 :> 5.077367641329531e-05 :> -7.20036873194064e-05 :> -3.7245153312760294e-05 :> 7.249856664305871e-05 :> 2.2414720687380852e-05 :> -6.155684145140234e-05 :> -7.664810105984746e-06 :> 2.85804248573473e-05 :> -3.6152309490646324e-08 :> 3.86526486767599e-05 :> -1.4006284245813091e-05 :> -0.00015120836046040963 :> 7.361032727845754e-05 :> 0.0003152579566734551 :> -0.00021195524189591408 :> -0.0005277210648487832 :> 0.0004703572783638681 :> 0.0007717574734980716 :> -0.0008954627919597703 :> -0.001012627857164383 :> 0.0015349575580967327 :> 0.0011943982184525286 :> -0.002432123228258949 :> -0.0012377957439342097 :> 0.0036197818250699866 :> 0.0010392111520942885 :> -0.005114324388627113 :> -0.0004703430147278584 :> 0.00691059332253219 :> -0.0006228059544207712 :> -0.008978362677236961 :> 0.0024241985527292402 :> 0.011261032711201649 :> -0.005160469774066745 :> -0.013676935125896208 :> 0.00913292632920996 :> 0.016123357472055417 :> -0.014794308598846265 :> -0.01848307417265467 :> 0.02293937546874407 :> 0.02063285839843857 :> -0.03523405731548666 :> -0.022453185292383104 :> 0.05602454640129296 :> 0.02383815920968249 :> -0.10138553138188472 :> -0.024704631737024998 :> 0.3167115011351708 :> 0.5250045350057191 :> 0.3167115011351717 :> -0.024704631737024647 :> -0.10138553138188545 :> 0.023838159209682245 :> 0.05602454640129442 :> -0.02245318529238117 :> -0.03523405731548606 :> 0.020632858398438054 :> 0.02293937546874406 :> -0.018483074172654032 :> -0.014794308598846393 :> 0.01612335747205424 :> 0.009132926329209059 :> -0.013676935125896086 :> -0.005160469774066614 :> 0.011261032711201845 :> 0.002424198552728965 :> -0.008978362677237601 :> -0.0006228059544210945 :> 0.006910593322532333 :> -0.0004703430147276999 :> -0.005114324388627051 :> 0.0010392111520945455 :> 0.0036197818250703288 :> -0.001237795743934232 :> -0.0024321232282593064 :> 0.0011943982184523566 :> 0.0015349575580969096 :> -0.0010126278571641848 :> -0.0008954627919598041 :> 0.000771757473497906 :> 0.00047035727836372234 :> -0.0005277210648488565 :> -0.0002119552418958731 :> 0.0003152579566736044 :> 7.361032727858147e-05 :> -0.0001512083604604247 :> -1.4006284245899888e-05 :> 3.865264867673136e-05 :> -3.6152309459163916e-08 :> 2.8580424857355213e-05 :> -7.66481010600899e-06 :> -6.15568414514097e-05 :> 2.24147206873927e-05 :> 7.249856664305469e-05 :> -3.724515331277384e-05 :> -7.200368731939395e-05 :> 5.0773676413330495e-05 :> 6.739792048057118e-05 :> -6.478374934755455e-05 :> Nil
We define our circuitry as
firCircuit x = fir firCoef x
Result of calculating response of circuit firCircuit can be presented as following graph
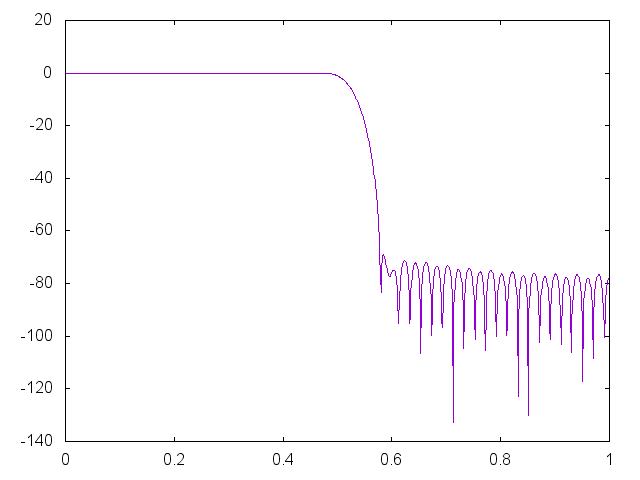
x axis represent frequency from 0 to Nyquist frequency and y is gain in dB. More details regarding ploting is available in testing code example available at github.
Details
Analysis can be precisely performed on acyclic circuits for both linear
and some nonlinear systems. By applying iterations it is possible to
analyze also cyclic circuits. Only restriction is that
circutry is defined by input type that is both Num and
Prependable.
Prepend is using polymorphic version of register called prepend.
Naive idea I started to work from is, that we push inside signal of complex numbers. Addition is addition of complex numbers and similar for multiplication. This should work fine at least for linear circuits.
Cyclic circuits can be are analyzed getting more values from output stream and waiting for result to converge. It works for analyzing iir filters.
For mixing/nonlinear circuits multiplication of spectrum is needed.
Multiplying two sin functions is expressed as following identity.
sin(a) * sin(b) = 1/2 (cos(a-b) - cos(a+b))
or when dealing in single frequency we get.
sin(x + a) * sin(x + b) ==
1/2 (cos(a - b) - cos(2x + a + b)) ==
1/2 (sin(a - b + pi/2) - sin(2x + a + b + pi/2))
Multiplying two signals on same frequency one with phase a and other with phase b results in signal decomposed in DC components and other with signal having double frequency.
Haskell type that holds phases on multiple harmonics can be
Map Int (Complex Double) Where Int represents harmonics and
Complex Double size and phase of a signal at that harmonics frequency.
In general Num class is needed for such type. That are function +
- and *.
acyclic circuits
What remains for such system is phase rotation. When we delay signal using register, we need to tell register how to delay input spectrum.
If circuit is acyclic, single value wrapped in type AnalyzerAcyclic is
enough for exact analysis. This represents type of input stream and is
type used as input and output of circuit.
data AnalyzerAcyclic s =
AnalyzerAcyclic {unAnalyzerAcyclic :: (Maybe (s -> s) , s)}
First type Maybe (s -> s) is spectrum transfer function. s -> s is
function for rotating input used by registerP function is wrapped in
Maybe, because instances of AnalyzerAcyclic for example
fromInteger and fromRational are unable to provide better than value
Nothing. For example function (+) requires forwarding valid
transform function as output. Second type s is input spectrum for
example Map Int (Complex Double) and represents amplitudes and phases
on all harmonics frequencies.
cyclic circuits
Simple example of cyclic circuit would be
integrator sig = r where
r = registerP 0 r + sig
registerP is polymorphic version of register called prepend from class
Prepenable with origin from prevous
post
and lack of theoretical foundations. Some care is required to avoid
bottom or infinite loop that would happen using AnalyzerAcyclic.
Current solution is that stream is used as input. In output stream we wait for values to converge. Type that works for our case is.
data Analyzer s = Analyzer {unAnalyzer :: ([Maybe (s -> s)] , Signal s)}
First value [Maybe (s -> s)] is list of spectrum transfer functions,
that is function that rotates input signal when register is reached.
Second type Signal s is stream of spectrum. For registryP is
required to retrieve spectrum transformation in breadth-first
order. Traversing
to spectrum rotate function s -> s in depth first order, would halt
evaluation and would reach bottom.
For this type we need to implement Ǹum instance.
Example of + is.
da + db = FreqAn (zipWith (<|>) fa fb, liftA2 (+) a b) where
(fa,a) = unFreqAn da
(fb,b) = unFreqAn db
That is, spectrum transfer function is generated by merging two spectrum
transfer functions one from argument da and other from db input. Addition
is done trough Applicative instance of underlaying input type that
needs to be instance of Applicative.
What next
Experimental library and some playground code in test.hs is available at
github. It is not yet
clear how to make Functor and Applicative instance of Analyzer and
family. Also Prependable typclass as used here and previously to
describe parallel circuits seems nice and useful, but has no theoretical
foundations I am aware of and for extra only law it I came up with is
broken in implementation of AnalyzerAcyclic. It is not clear what kind
of nonlinear circuits beside frequency mixers are possible to analyze
using such approach. There is missing bunch of utility functions and
overall many questions remains open.
Fell free to reach me over git or irc at irc.freenode.com. I am hanging on channels #haskell and #clash-lang under nick ralu but you can also send mails on address starting with luka and ending with name of this domain.